This puzzle concerns the painting of the four sides of a tetrahedron, or triangular pyramid. 
If you cut out a piece of cardboard of the triangular shape shown in Fig. 1, and then cut half through along the dotted lines, it will fold up and form a perfect triangular pyramid. 

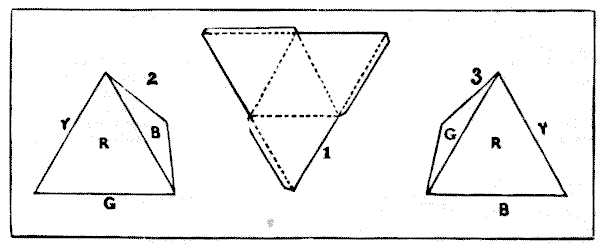
In how many different ways may the triangular pyramid be coloured, using in every case one, two, three, or four colours of the solar spectrum? 
Of course a side can only receive a single colour, and no side can be left uncoloured. 
But there is one point that I must make quite clear. 
The four sides are not to be regarded as individually distinct. 
That is to say, if you paint your pyramid as shown in Fig. 2 (where the bottom side is green and the other side that is out of view is yellow), and then paint another in the order shown in Fig. 3, these are really both the same and count as one way. 
For if you tilt over No. 2 to the right it will so fall as to represent No. 3. 
The avoidance of repetitions of this kind is the real puzzle of the thing. 
If a coloured pyramid cannot be placed so that it exactly resembles in its colours and their relative order another pyramid, then they are different. 
Remember that one way would be to colour all the four sides red, another to colour two sides green, and the remaining sides yellow and blue; and so on.